Decimal Bank Vault Crack
The brute force attack for the decimal vault is almost ready. All you have to do is add ’2’, ’3’, ’4’, and ’5’ to the digits list. The nested loops automatically go through all the items in the digits list regardless of how many items it contains. So, instead of eight combinations, the updated list will cause the script to try up to 216 combinations.
Example script: decimal_bank_vault_crack.py
- Open the bank_vault_crack script with the micro:bit Python Editor.
- Change the project name to decimal_bank_vault_crack.
- Make the changes shown in the decimal_bank_vault_crack script shown below.
- Save and then click Send to micro:bit to flash the script into the PIN Pad micro:bit.
- Press the A button to start the decimal brute force attack on the decimal bank vault.
# decimal_bank_vault_crack.py # <- change
from microbit import *
import radio
radio.on()
radio.config(channel=7)
# digits = ['0','1'] # <- comment (before change)
digits = ['0','1','2','3','4','5'] # <- change
display.show(Image.ARROW_W)
while True:
if button_a.was_pressed():
display.clear()
for a in digits:
for b in digits:
for c in digits:
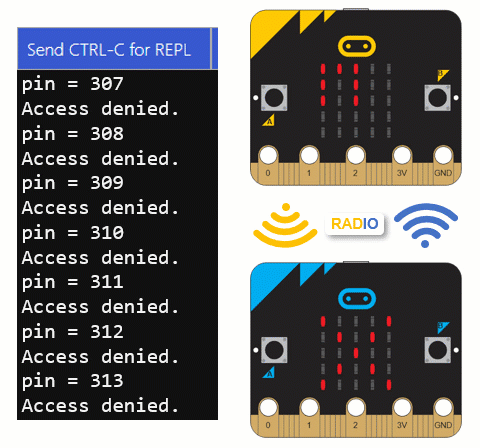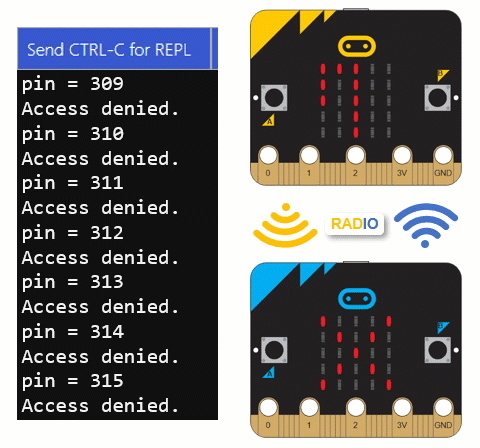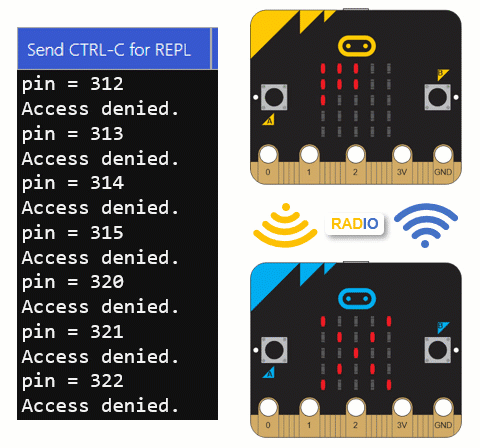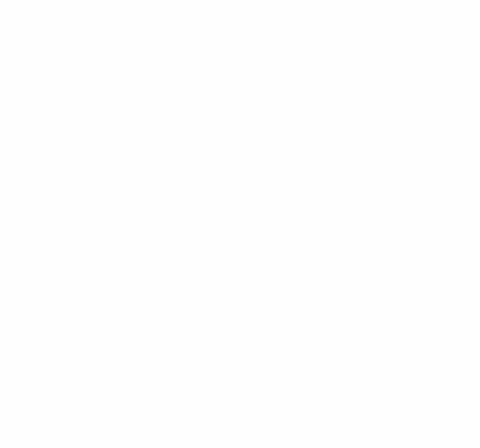
pin = ''.join([a, b, c])
print("pin =", pin)
for x in range(3):
for y in range(int(pin[x])):
display.set_pixel(x, y, 9)
response = None
while response is None:
radio.send(pin)
sleep(100)
response = radio.receive()
print(response)
if response == "Access granted.":
while True:
display.scroll(pin)
sleep(4000)
display.clear()
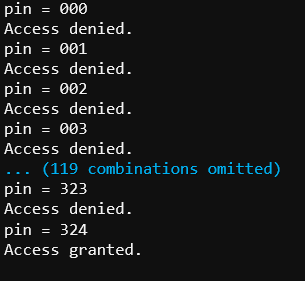
- Verify that the decimal_bank_vault_crack script is trying the various combinations.
The Math
While you are waiting for the crack script to succeed, let’s calculate how long it will take.
Since each digit counts from 0 to 5, that’s 6 possible digits: 0, 1, 2, 3, 4, and 5. After the right digit has counted through its 6 possibilities, the middle digit increases by 1, and the right digit has to start over. All told, the two right digits have 6 x 6 = 36 combinations. The third digit also has 6 possibilities, and for each of those, the right two digits must go through all their combinations. So, that’s 6 x 36 = 216.
More generally, if p = number of possible values for each digit, d = the number of digits, and c = the number of combinations, you can calculate the possible values like this:
c = pd
Let’s try it with p = 6 and d = 3. That’s:
c = 63= 216.
Now, remember that there’s a 4 second delay between each try. So the number of seconds for all combinations would be:
216 x 4 seconds = 864 seconds.
846 seconds x ( 1 minute / 60 seconds ) = 14.4 minutes.
Also, to reach 324, the decimal bank vault crack will have to go through this many combinations:
Digit-left : 3 repetitions x 36 = 108
…because the middle and right digits have to go through their cycles for each time the left digit increases by 1.
When digit-left = 3, that’s the fourth repetition, and the right digits still have some cycles.
Digit-middle needs to go through 2 more cycles, x 6 for the right digit = 12
On the middle digit’s 3rd cycle, the right digit has to count 0, 1, 2, 3, 4, which is 5 repetitions.
Total: 108 + 12 + 5 combinations = 125 combinations.
In terms of minutes, that’s:
125 combinations x 4 seconds/combination x (1 minute / 60 seconds) = 8.33 minutes.
What happens if you increase the number of digits to 4?
Answer: _______ (216 x 6 = 1296)
What’s the longest a brute force attack would take in that case?
Answer: _______ (1296 combinations x 4 seconds/combination = 5184 seconds. 5184 seconds x 1 minute / 60 seconds = 86.4 minutes. That’s over 1 hour and 26 minutes.)
