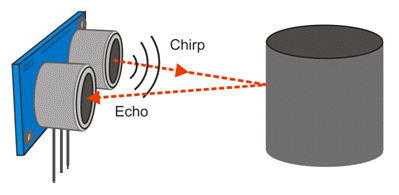
The PING))) Ultrasonic Distance Sensor works by making a high-frequency chirp, then measuring the amount of time it takes to hear the return echo. So, its measurements are dependent upon the speed of sound in air.
The speed of sound changes with air temperature, humidity, and even air quality. Neither humidity nor air quality make enough of a difference to figure into PING))) sensor distance calculations. Air temperature, on the other hand, can cause measurable distance errors. The speed of sound increases by 0.6 meters per second (m/s) for every degree-Celsius (°C) increase in temperature. Since the speed of sound is about 331.5 m/s at 0 °C, we can use this equation to calculate the speed of sound at a given temperature:
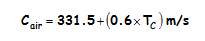
Converting from °F to °C and Vice Versa
To convert a degree-Fahrenheit to Celsius, subtract 32 from TF (the Fahrenheit measurement), then divide by 1.8. The result will be TC, the Celsius equivalent. To convert from Celsius to Fahrenheit, multiply TC by 1.8 and then add 32. The result will be TF

Below are examples for the speed of sound at two fairly comfortable, but slightly different indoor temperatures.
Example 1: Calculate the speed of sound at 22.2 °C, which is approximately 72 degrees Fahrenheit (°F).
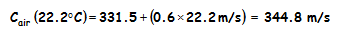
Example 2: Calculate the speed of sound at 25 °C, which is 77 degrees Fahrenheit (°F).
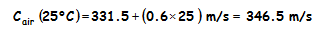
How much of a difference does this make to your distance measurements? We can calculate the percent error this will propagate with the percent error equation.

If the predicted temperature in the room is 72 °F (22.2 °C), and the actual temperature is 77 °F (25 °C), then the error is 0.49 percent. Half a percent error would require that you move the object half a centimeter beyond 100 cm before it would transition from 99 to 100 cm.

