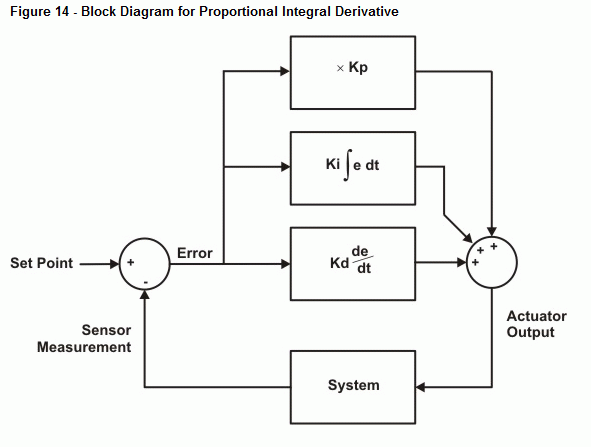
A PID control loop involves some contributions from each of the three kinds of control: proportional, integral, and derivative. The amount of contribution that each of the controls makes can be adjusted by changing their proportionality constants, Kp, Ki, and Kd. By making these constants larger or smaller, you can make the contribution of one of the controls more dominant or subtle in the system. One system might need only light integral control, some proportional and strong derivative, while another system might need strong integral and proportional controls, but not much derivative, while still another system might need roughly equal measures of each.
Here are several important things to keep in mind when working with PID control loops:
- Error is the difference between the level you want and the level that is measured, and control loops work to correct error.
- Proportional control resists error by applying an opposing influence that is proportional to the error.
- Integral control detects and corrects trends in error over time.
- Derivative control detects and resists abrupt changes in the system.

The next example program will perform this PID control loop. To make comparisons easier, Kp, Ki, and Kd are all set to 10.
Example Program - PidAlgorithm.bs2
Keep in mind that proportional always does some work when there's some error. However, integral and derivative are ready to do extra work to correct the error, integral to correct trends, and derivative to correct abrupt changes.
- Enter, save, and run PidAlgorithm.bs2.
- Here is a series of sensor inputs that the integral control will detect as a trend and resist much more strongly than either proportional or derivative: 1 2 3 4 5 5 5 5 5 5 5 5 5
- Here is a series of sensor measurements that derivative will work hard to correct while proportional and integral don't do nearly as much: 3 -3 4 -4 5 -5 6 -6 5 -5 4 -4
' PidAlgorithm.bs2
' Demonstrates how a combination of proportional, integral, and
' derivative control influence error correction in a feedback loop.
' {$STAMP BS2}
' {$PBASIC 2.5}
SetPoint CON 0 ' Set point
Kp CON 10 ' Proportionality constant
Ki CON 10 ' Integral constant
Kd CON 10 ' Derivative constant
Current CON 0 ' Array index - current error
Accumulator CON 1 ' Array index - accumulated error
Previous CON 2 ' Array index - previous error
Delta CON 3 ' Array index - change in error
sensorInput VAR Word ' Sensor input variable
error VAR Word(4) ' Four different types of errors
p VAR Word ' Proportional term
i VAR Word ' Integral term
d VAR Word ' Derivative term
drive VAR Word ' Output
DO
DEBUG "Enter sensor input value: "
DEBUGIN SDEC sensorInput
' Calculate error.
error(Current) = SetPoint - sensorInput
' Calculate proportional term.
p = Kp * error(current)
' Calculate integral term.
error(Accumulator) = error(Accumulator) + error(Current)
i = Ki * error(Accumulator)
' Calculate derivative term.
error(Delta) = error(Current) - error(Previous)
d = Kd * error(delta)
' Calculate output.
drive = p + i + d
' Display values.
DEBUG CR, CR, "ERROR", CR,
SDEC ? SetPoint, SDEC ? sensorInput, SDEC ? error(Current), CR,
"PROPORTIONAL", CR,
SDEC ? Kp, SDEC ? error(Current), SDEC ? p, CR,
"INTEGRAL", CR,
SDEC ? Ki, SDEC ? error(accumulator), SDEC ? i, CR,
"DERIVATIVE", CR,
SDEC ? Kd, SDEC ? error(Delta), SDEC ? d, CR,
"OUTPUT", CR,
SDEC ? p, SDEC ? i, SDEC ? d, SDEC ? drive, CR, CR
' Save current error to previous error before next iteration.
error(Previous) = error(Current)
LOOP
Your Turn - Tuning the PID Control Loop
Assume that your sensor inputs will range from -10 to 10. Adjust your constants (Kp, Ki, and Kd) so that the maximum contribution any of the controls can make to the output ranges from 650 to 850. To get the integral control to adhere to this requirement, you will also have to use the MIN and MAX operators.
