Series vs. Parallel Resistance
Imagine you are inventing something, and your design needs a 1220 Ω resistor, or maybe a 500 Ω resistor, but your kit doesn’t have either of those! Not to worry, you can combine resistors in various ways to get resistance values that are not in your kit.
Resistors can be connected end-to-end (in series) or side-by-side (in parallel). Both series and parallel resistances can be boiled down to individual equivalent resistance values. This section will show you how.
Series Resistors
When resistors are connected end-to-end, they are connected in series. The total resistance is simply the sum of the resistors. Just add them up, and that’s the resistance.
For 2 resistors, that would be R = R1 + R2.
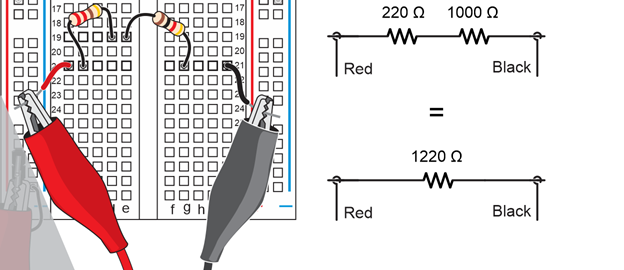
Example: Calculate the resistance of a 220 Ω resistor in series with a 1000 Ω resistor.
Solution: R = 220 Ω + 1000 Ω = 1220 Ω.
If we have some number N of resistors, the total resistance would be R = R1 + R2 + … + RN.
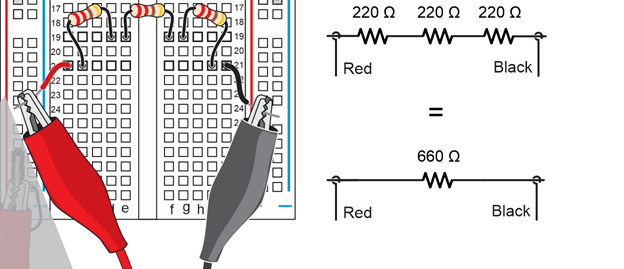
Example: Calculate the resistance of three 220 Ω resistors in series.
Solution: R = R1 + R2 + … + RN = 220 Ω + 220 Ω + 220 Ω = 660 Ω
In this solution, since all the resistor values are the same, you could just multiply 220 x 3.
Parallel Resistors
Resistors can also be connected in parallel which is side-by-side, with only two connection points where all the resistor leads are connected. (Remember, you can use a row-of-five sockets in the breadboard’s terminal strip to connect resistor leads together.)
In the special case of two resistors in parallel, the equation is R1 * R2 / (R1 + R2). For more than two, the equation is 1/(1/R1 + 1/R2 + … + 1/RN).
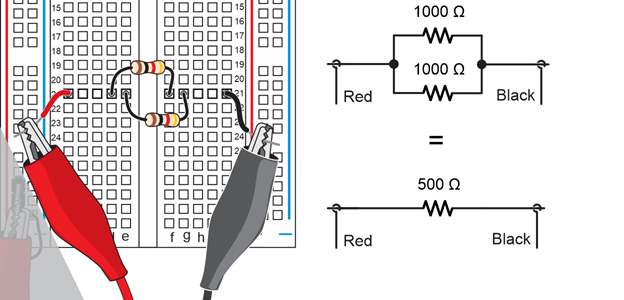
Example: Calculate the resistance of two 1000 Ω resistors in parallel.
Solution: R = R1 x R2 / (R1 + R2) = (1000 x 1000) / (1000 + 1000) = 1,000,000 / 2000 = 500 Ω
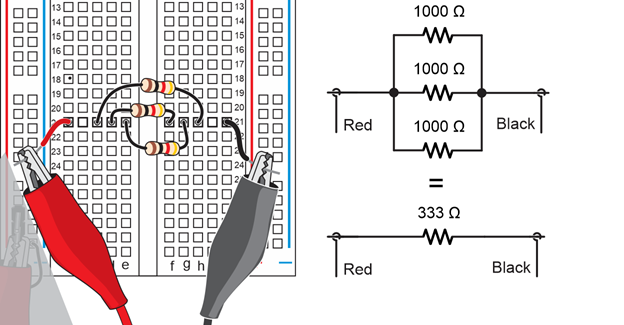
Example: Calculate the resistance of three 1000 Ω resistors in parallel.
Solution R = 1 / (1/R1 + 1/R2 + …+ 1/RN) = 1 / (1/1000 + 1/1000 + 1/1000) = 1 / (3/1000) = 1000/3 ≈ 333 Ω.
Series Parallel Combinations
To figure out the equivalent resistance of a circuit with both series and parallel elements, calculate the equivalent resistance of a subcircuit that is either parallel or series first.
For example, if one resistor is in series with a pair of parallel resistors, solve for those parallel resistors first. After that, all that’s left is two resistors in series.
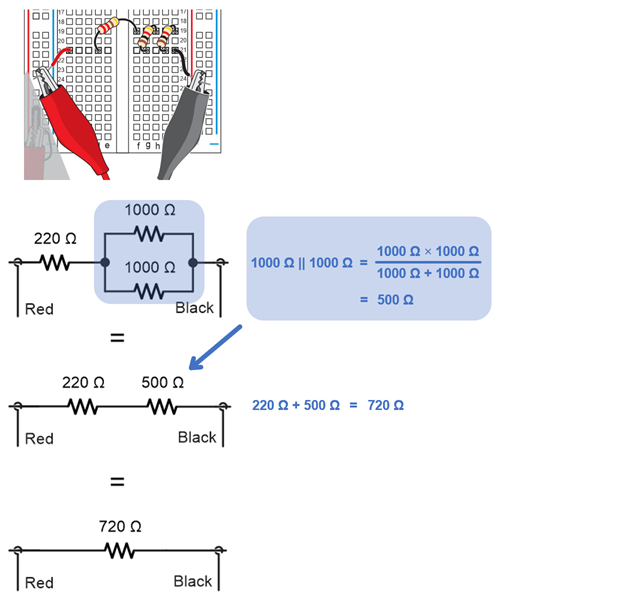
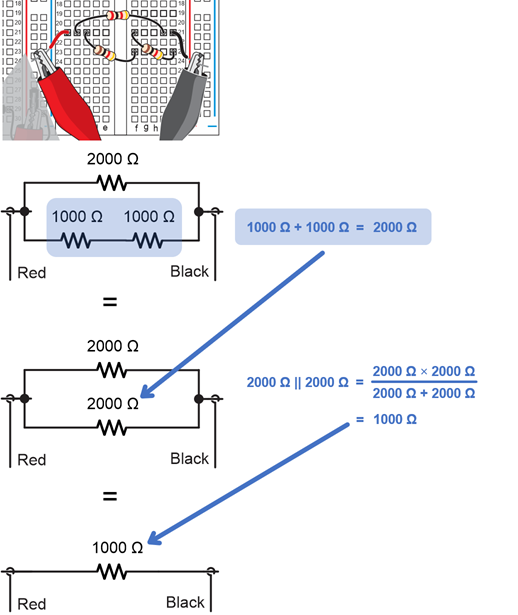
Another example, let’s say that one resistor is parallel to a pair of resistors in series. In that case, solve for the series resistors first. Then, all that’s left are two parallel resistors.
Your Turn - Series and Parallel Calculations
- Calculate the resistance across each of these parallel and series combinations.
- Then, build each one on the breadboard and measure it with the CYBERscope to verify your results.
Series
- 1000 Ω + 1000 Ω
- 220 Ω + 220 Ω
- 220 Ω + 220 Ω + 220 Ω
Parallel
- 1000 Ω || 1000 Ω
- 220 Ω || 220 Ω
- 220 Ω || 220 Ω || 220 Ω
