As we said before, the circle is special because we can approach it as a regular polygon with 36 (or more) vertices.  We will use exactly 36 vertices for this example.

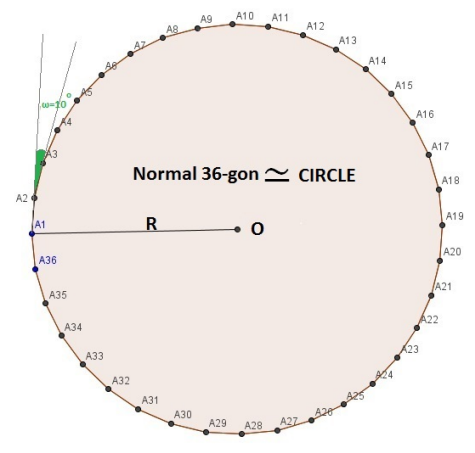
So, if we want the robot to do a circle (clockwise) we need to give the following commands (note: the exterior angle values may be difficult to see in the image but each is 10 degrees):

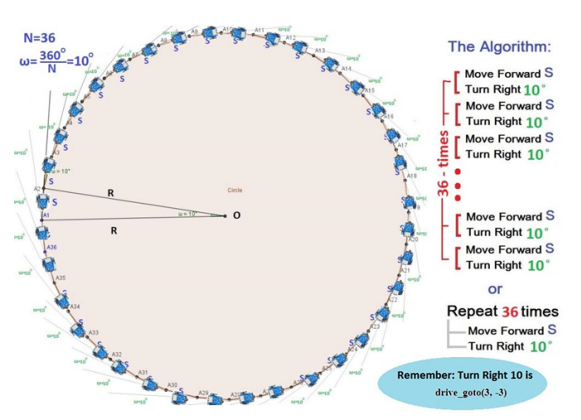
Keep in mind that the S mustn’t be a big number because otherwise your circle will be very large! Choose small numbers for the S values. For example, in the next example S = 8 ticks.

The following SimpleIDE code programs the ActivityBot to make a circle with radius of approximately 15 cm:

• Start a new SimpleIDE Project
• Enter in the code below and make sure load it to your robot with the "Load EEPROM & Run" button

The question that might arises from this example is: what length should the S be in order to make a circle with a specific radius (R)? In other words, can I calculate the S as a function of R? Math theory shows us that “Cosines Law” is the answer to this. Looking at the triangle OA1A2 (below) we can see that:

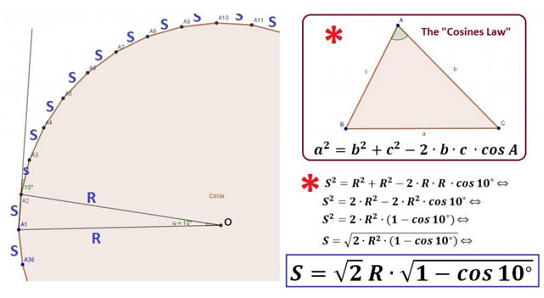
So now we are almost ready for the final algorithm that will be able to create any circle with a given radius R, or create a polygon within a circle of radius R.