Angle and Angular Velocity

Did You Know? Angular Velocity

Up to now, your scripts have controlled the servo horn’s angle.  That’s the direction the horn points, measured from 0° to 180° of its range.  Your scripts can also control the angular velocity.  That’s how fast the horn turns when it’s moving from one position to another.

Control Angular Velocity with the Script

The scripts currently have the angular velocity slowed down with statements like:

        value = value + 1

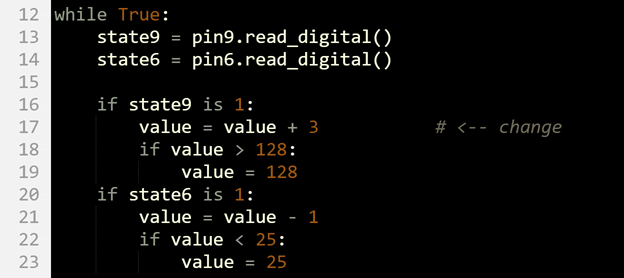
While pressing and holding the P9 button, the value variable increases by 1 every 50th of a second.  In response, the servo horn increases its angle by about 1.75° per 50th of a second.  If value = value + 1 is changed to value = value + 3, the modified script will make the horn turn 3 times as fast while the P9 button is pressed and held.  This is an example of changing the horn’s angular velocity.        

Think back to the first servo control script.  It took the servo some time to turn to each new position.  In that example, the servo turned to each new position at top speed.  If your script advances the value variable faster than the servo can turn, it will catch up eventually.  Just keep in mind that increasing the number in the value = value + number statement can only go so far to speed up the servo since the servo has a mechanical speed limit as well.  

Angle vs. Angular Velocity

Angles can be measured in degrees.  The symbol for angle is the Greek letter theta Θ .  Angles can be expressed in degrees like this: Θ = 30°.  

  • Quantity name: Angle
  • Quantity symbol: Θ
  • Unit name: Degree
  • Unit symbol: °
  • Description: A degree 1/360 of a full circle’s worth of deviation

Angular velocity is a measure of how fast (and in which direction) something turns.  Angular velocity can be measured in degrees per second.  Counterclockwise rotation is considered positive, and clockwise negative.  In other words, if the angle is increasing, angular velocity is positive.  If angle decreases over time, angular velocity is negative.  The symbol for angular velocity is the Greek letter omega, ω, and one way angular velocity is expressed is in degrees per second with this notation: °/s.    

  • Quantity name: Angular velocity
  • Quantity symbol: ω
  • Unit name: degree per second
  • Unit symbol: °/s
  • Description: Change in angle over time.  A degree per second is 1/360th of a full circle of rotation per second.

When angular velocity is constant it can be measured as the change in angle over time.  Change in angle can be measured as the final angle Θf minus the initial angle Θi divided by the time t it took for the object to rotate that far.

ω = (Θf - Θi) / t

Example: If it takes 2.1 seconds for the horn to rotate from 0° to 180°, what is its angular velocity?

ω = (Θf - Θi) / t
    = ( 180° - 0°) / 2.1 s
    ≈ 85.7° / s

Example: If it takes 1.05 seconds for the horn to rotate from 135° to 45°, what is its angular velocity?

ω = (Θf - Θi) / t
    = ( 45° - 135°) / 1.05 s
    ≈ -85.7° / s

Your Turn: Change Angular Velocity

Let’s try increasing the counterclockwise angular velocity to 3-times the original.  After this change, the servo horn should take about ⅓ of the time it originally took to turn from 0° to 180°.   

  • Reopen your saved copy of servo_buttons_control.hex
  • Click Load/Save.
  • Click Or browse for a file.
  • Select servo_buttons_control.hex, and then click Open.
  • Set the Script Name field to servo_buttons_control_faster_ccw.
  • In the if state9 is 1 block, change the value = value + 1 statement to value = value + 3.
  • Click Load/Save, and then click Download Project Hex to save your work.  
  • Close the Load/Save dialog box after downloading the .hex file.

 

 

  • Add batteries to the  battery pack connected to the Edge I/O Adapter.
  • In the python.microbit.org/v/2 editor, click Connect, and then click Flash.   
  • Press and hold the P6 pushbutton until the servo reaches its 0° limit
  • Press and hold the P9 pushbutton to make the servo turn to its 180° limit, and observe the rate the horn turns.
  • Observe the rate the horn turns as you press and hold the P6 pushbutton to make the servo turn to its 0° limit.  Did it turn from 0 to 180° in about ⅓ the time it turned from 180° to 0°?  That means it’s turning 3 times as fast.
  • Remove the batteries from the battery pack.