For ActivityBot navigation, the raw sensor values aren't directly useful. What matters is the difference between the light levels detected by each sensor so that the ActivityBot can turn to the side of the one sensing brighter light. It is also nice to have values that will fall into a predictable range that can add or subtract them from the speeds sent to drive the servo motors.
Accomplishing this takes just a few steps - after building the equation you need, you'll then figure out how best to use blocks that follow this equation.
The concept is simple - of all of the light detected by both sensors, which portion of it is coming from the right sensor (and if you need to, you can tell which portion is coming from the right sensor). First, divide one sensor measurement into the sum of both. The result will always be in the 0 to 1 range. This technique is an example of a normalized differential measurement. Here’s what it looks like as an equation:

A range from 0 to 1 still isn't useful - especially in Blockly, since we can't use decimal or fractional numbers. The goal is to have a range from -100 to +100 (a range with 200 possible values). Multiplying the normalized differential measurement by 200 will give a result between 0 and 200. Subtracting 100 from that result will provide a range from -100 to +100. If the phototransistors sense the same level of light, regardless of how bright or dim, the final whole number will be zero. This is an example of a zero-justified normalized differential measurement, let's call it "ndiff" for short. Now our equation looks like this:
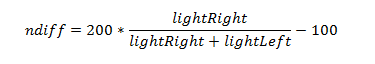
We have to be careful in BlocklyProp. Because all math is done with integers, it is possible to create an equation that always results in zero.
Preserving values in integer math
A good habit is to make your value bigger before you make it smaller. If you can use decimals or fractional values, it doesn't matter if you divide then multiply or multiply then divide. When doing integer math, it DOES matter. If we do the multiplication first, we can preserve the value of our result:
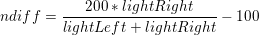
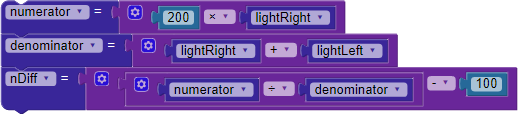
To turn this into blocks, you'll create a few different quantities. The top part of the fraction (the numerator) becomes:

The bottom part of the fraction (the denominator) becomes:

Which means nDiff is:
The example code below will display the lightRight and lightLeft measurements, and also show the value of nDiff as an asterisk. This makes it easier to visualize how the ActivityBot navigation program uses the sensor values to aim for a new trajectory towards the brighter light.
Graphical Test Code
- In your BlocklyProp account, create a new project named Light Sensor Test Graphical.
- Build the project shown below, and save it.
- Click the Run Once (Load to RAM) button.
- Rotate the ActivityBot towards and away from a light source to see the position of the asterisk change.

When the Terminal opens, you should see something like this:

How it Works
The graphical display was generated using Terminal print number and character value blocks.
This program builds on Test Light Sensors from the previous page. Two more variables are declared in addition to lightLeft and lightRight: nDiff and position. nDiff holds the result of the fancy-named equation, and position is used to print a graphical display that represents the value of nDiff.
After calculating nDiff, its result needs to be turned into a position in the terminal. nDiff can be any number from -100 to +100, and we need positions from 0 to 50 (that's about how many characters wide the Terminal window is).
To get from (-100 to +100) to (0 to 50), we first add 100 (bringing it to 0 to 200), then divide by 4 (bringing it to 0 to 50).
Then, using a repeat x times block, we use the Terminal print number and character value blocks to print enough spaces to push out the asterisk (*) we are planning to print it where it needs to be on the Terminal screen.
Did You Know?
Integer math, nesting, and order of operations all matter. Just like with normal mathematical operations in real life, multiplication and division operations are performed before addition and subtraction. However, you may have already learned that Blockly evaluates each block from "inside-out," and you have to plan accordingly to get the correct result.
Dealing with integer math can be tricky, too. Most modern microcontrollers can do floating-point math, including the Propeller Multicore microcontroller. BlocklyProp doesn't support it, however, because the blocks themselves are not able to tell what kind of number - integer or floating-point - your variable might be. In addition, floating-point operations are slower and take up more memory than integer operations.
Once you know a few tricks, it's easy to overcome this limitation.
Try This
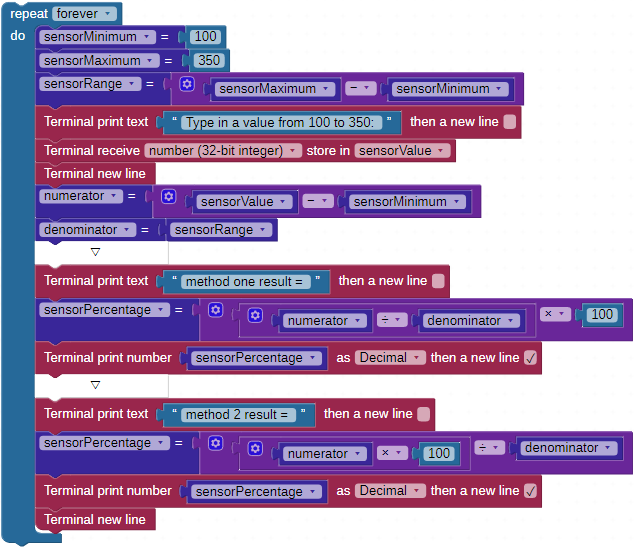
There may be times where you want to turn the value of a sensor into a percentage. To change a sensor's value to a percentage, we have to know what it's minimum and maximum values are. The difference in those values is the sensor's range. Then, you can use the following formula to convert the sensor's value to a percentage:
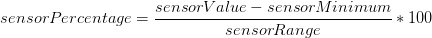
In real life, because multiplication and division have the same operator precedence, either of these calculation steps will get you the same result:
- Subtract sensorMinimum from sensorValue, next divide that by sensorRange, then multiply that by 100.
- Subtract sensorMinimum from sensorValue, next multiply that by 100, then divide that by sensorRange.
To see what difference your order of operations can have on the result in integer math, try the following example:
- Close the Test Light Sensor Graphical project.
- Click New Project, name it something like Integer Math Operator Order.
- Enter the code shown below, click Run Once (Load to RAM).
- Click in the Terminal window and try typing in different values.
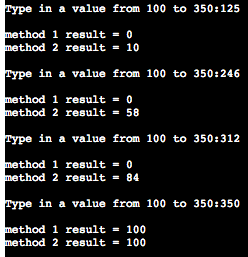
- Compare the results. What's happening?
Here's why this happens:
What percentage of 200 is 150? To find out, you might take 150 divided by 200 and get 0.75, then multiply that by 100 to get 75.
But what is 0.75 as an integer? Here's a hint: it's not 1. In integer math, the decimal is truncated. This means that the number is cut off at the decimal, leaving only 0. If you're trying to convert to a percentage by multiplying by 100, 100 times 0 is still 0.
If we use the same numbers, but this time multiply first by 100 before dividing by 200, we get 150 times 100 = 15000, then 15000 divided by 200 = 75.
Your Turn
- Using what you know about integer math and building a graphical display in the terminal, try making a graphical display that shows the result of each sensor as its marker. You could use "x" for the left light sensor and "o" for the right one.
- Try printing a number as a decimal to the Terminal. For example, how would you print 1562 millimeters as 1.562 meters in the Terminal using BlocklyProp when only integers are allowed? Here's a hint: if you divide 1562 by 1000, your left with 1. 1 times 1000 is 1000 and using subtraction you can find the rest of the number.
