Forces

There are forces all around us - the force of gravity pulls us downward, wind pushes from the side, magnets pull on metal, and water pushes up a beachball to make it float. A force is any kind of push or pull - when a force is applied to an object, that object speeds up.

You might be thinking, “if forces make me speed up, then why isn’t gravity making me speed up?” The answer is that there is another force, the ground pushing you back up with an equal amount of force. The result is that you do not move.

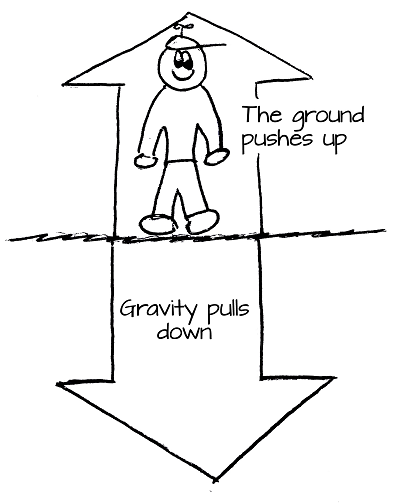
Objects almost always have a set of forces that act on them at any given time. In order to determine how much an object will speed up or slow down and in what direction, you’ll have to determine each of the individual forces that are acting on an object and add them all together.

Adding two forces together isn’t as easy as adding two numbers together because forces are more than just a size. Forces also have a direction. To represent a force, we use a vector. A vector contains both size and direction, and can be drawn using an arrow. The arrow can point in any direction and its length represents the size of the force. Other things can be represented with vectors as well. When speed and direction are combined, it is called velocity, and velocity can be represented with a vector.

Using vectors, we can add the forces of two soccer players kicking a soccer ball at the exact same time, and predict which way soccer ball will go:

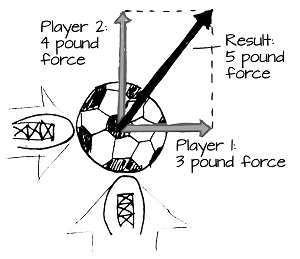
Where did the 5 pound answer come from? Hint: re-arrange the 3 and 4 pound vectors to make a triangle. Then, use the Pythagorean Theorem to find the length of the result. If you know how to calculate angles with Tangent, you can find the exact direction of the resulting force as well!

Try This

Below are a few problems to help you practice learning how to use vectors to find resultant velocities.

• An airplane is flying due east at 240 miles per hour (MPH).  Suddenly, 70 MPH wind begins blowing due north. Find the resulting velocity (speed and direction) of the airplane. Hint: Draw the velocity of airplane and that of wind as vectors (arrows whose length is proportional to the size or magnitude of the thing they represent and with a tip and a tail to help represent their direction).  Then rearrange these vectors tip to tail to form a triangle and calculate the resultant using Pythagorean theorem. 
• You are paddling a canoe east on river at a speed of 4 miles per hour (MPH). The river flows 10° south of east at 1.5 MPH. What is the resulting speed and direction of your canoe?
• The target for a quadcopter is in a north east direction. It is flying towards it with a velocity of 10 miles per hour (MPH). A strong gust of wind starts blowing in the southern direction at a velocity of 5 MPH. Calculate the change in velocity of the quadcopter after the wind starts blowing.

Your Turn

Try creating your own scenarios like the ones in the problems above.  Remember that vectors can be used to represent anything that has both size (magnitude) and direction, including velocities and forces.  What other measurable properties can be represented by vectors?