Mimicking Control Surfaces

By varying the amount of lift produced on different parts of the aircraft, the aircraft can tilt or turn to change its motion. On an airplane, there are a set of flaps called control surfaces that alter the amount of lift and/or push on the air flowing past the airplane, causing it to tilt or turn.

The set of flaps at the rear edge of the wings on an airplane are called ailerons. They are used to tilt the airplane sideways by causing one wing to push up and the other wing to push down. This motion is called roll. Rolling allows the airplane to turn:

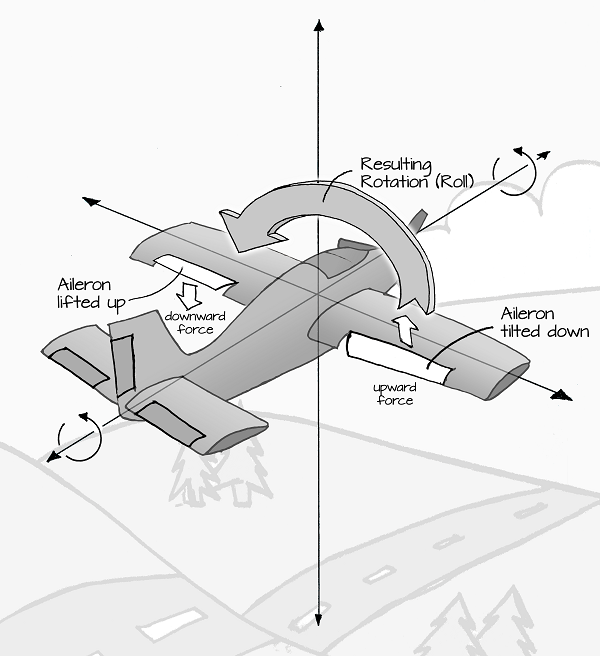
Multirotor aircraft like quadcopters don’t have control surfaces like airplanes so, but they are able to roll by speeding the motors up to generate more lift on one side and slowing down the motors to generate less lift on the other, causing a controlled tip that results in a roll:

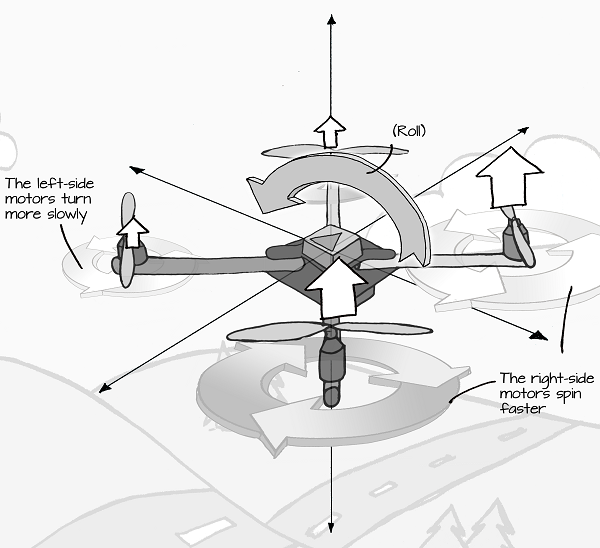
When a multirotor aircraft rolls, it begins moving sideways, which is a type of lateral movement. Lateral movement refers to any movement that is parallel to the ground. Another type of lateral movement is caused with a multirotor pitches. Pitch refers to the amount of forward and backward tilt. On an airplane, control surfaces called elevators are used to push up or pull down on the tail of the airplane, causing it to tilt up or down. Airplanes use this movement to climb or dive:

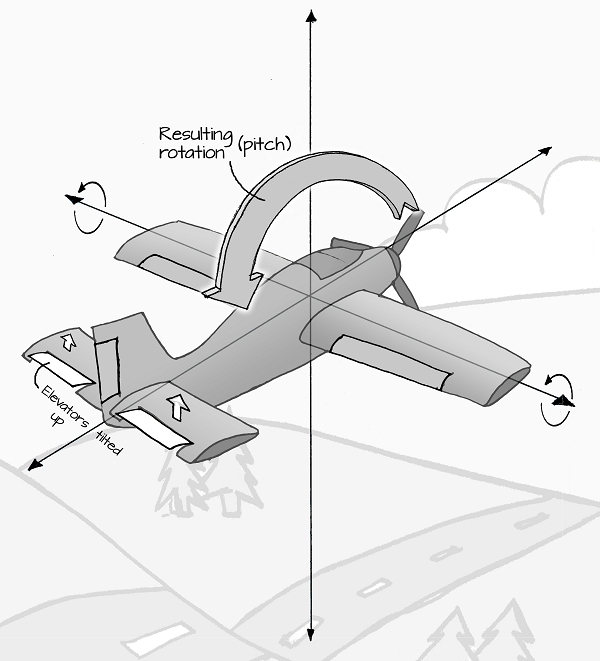
Multirotors use pitch to move forward or backward: 

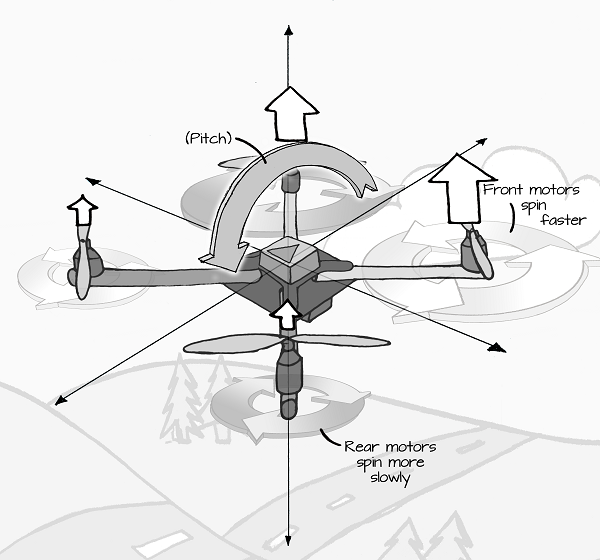
Thrust as a Vector

Remember how forces are vectors? When the multirotor is rolled to the side, some of its thrust is now pulling it sideways, and less of it is pulling it upward:

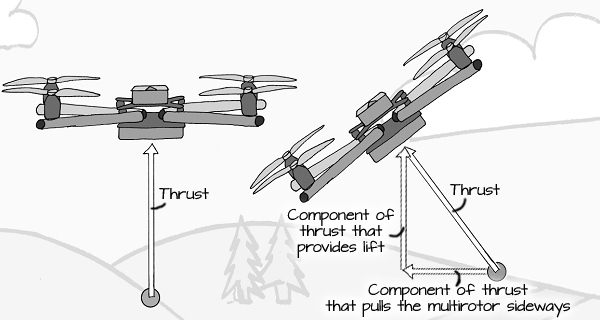
Just like two forces can add together to become a single force in a new direction, a single force can be broken into multiple component forces - for instance, we can break down the thrust of a tilted multirotor to analyze both the part of the thrust that is still providing lift, and the part of the thrust that is pulling the multirotor to the side.

Notice that the part of the thrust that is lifting the multirotor is smaller? If the total amount of thrust is not increased, it will begin to fall because the thrust is no longer providing enough lift to counteract the pull of gravity:

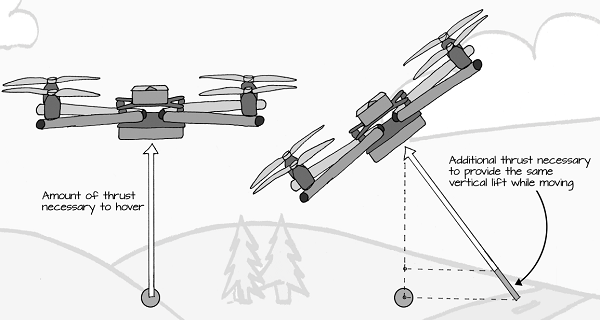
How much additional thrust is necessary?  To answer that question, we'll use some right-angle trigonometry.  First, we have to know how much thrust is being put out by the quadcopter.  If it is hovering, then the amount of thrust is equal to the weight of the quadcopter (remember: forces add up, and weight and thrust/lift cancel each other out if it's not accelerating upward or downward.)  For this example, we will say that the thrust is 3 pounds.

The other thing we need to know is the new angle of the thrust.  For this example, we will use a 30° tilt.

Draw out the triangle with the angle of 30° at the top and the vertical leg with a length of 3:

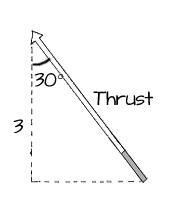
Next, we'll use the cosine function to determine the length of the side representing the thrust.  The cosine function describes the relationship between an angle and the ratio of the side adjacent to the angle and the hypotenuse (the longest side of a right triangle).  When we do the math, we get:

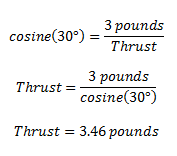
This means that an additional 0.46 pounds of thrust is required to keep the quadcopter at the same height.

We can use this same type of math to find out how large or small the sideways (horizontal) component of the thrust is.  Just like the cosine function describes the relationship between the adjacent side and hypotenuse, the Tangent function describes the relationship between the adjacent and opposite sides of the triangle.  If we find the length of the opposite side, we will know how large the sideways component of the thrust is:

Your Turn

Try calculating the additional thrust necessary for multirotors of different weights with tilts at diffferent angles.  If your calculator has a cosine (abbreviated cos) button, make sure your calculator is in degree mode.

Try making paper airplanes with differnt types of control surfaces.  Bend or fold the control surfaces in different ways to observe how your paper airplane pitches, rolls, and tilts.

Educators: for additional resources and practice problems, search online for "forces at an angle"