Trigonometry is used to calculate the rotation angle. Even if you haven’t studied it yet, try to follow along. It's pretty neat!
A triangle with a 90° angle (called a right triangle) can have one of its corners marked θ (Greek letter theta) to represent the angle there. Of the right triangle's three sides, the one is opposite of θ, one adjacent to θ forming the right angle, and the hypotenuse is the side that connects the other two. The diagrams will use the shorthand opp, adj, and hyp for these sides.

In trigonometry, the ratios of each pair of sides have names: sine (sin), cosine (cos), and tangent (tan). For each angle of θ, the ratio for sin, cos, or tan will be the same, regardless of the size of the triangle. Scientific calculators have sin, cos, and tan keys to complete the division calculation for you, and all you have to do is give it the angle. Python’s math library has methods for calculating these as well.
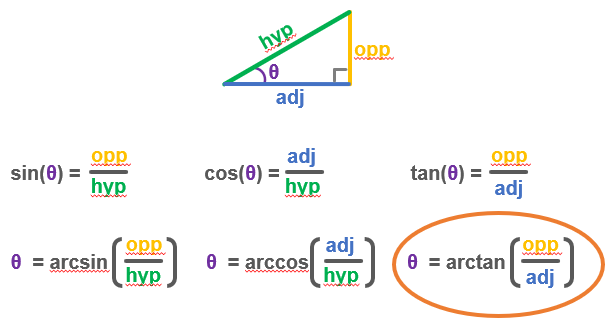
If you only know the result of a division, like opp / adj, you can get the angle θ with the arctan calculation. That’s also called the inverse tangent. Calculators often have tan-1 key for calculating this, and Python’s math module has the atan and atan2 methods.
The arctan calculation is particularly useful for calculating the micro:bit’s rotation angle. All your script needs is the amount of gravity acting on the x and y accelerometer axis. Treat the y-axis measurement as the opposite side and the x-axis measurement as the adjacent side of a right triangle, and the arctan calculation will give you the angle θ.
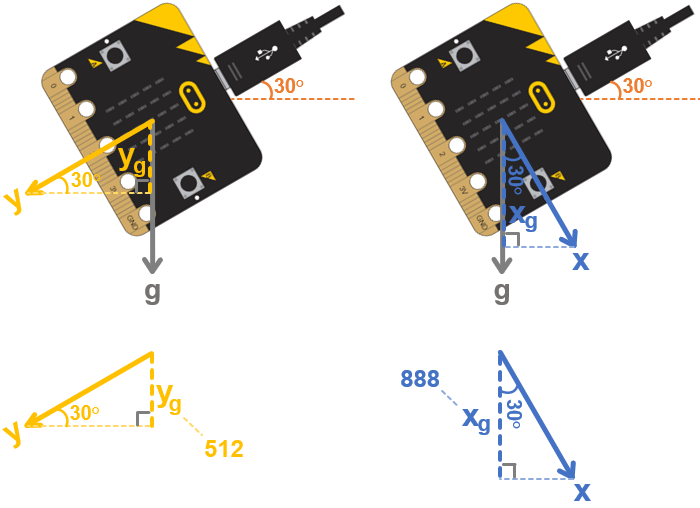
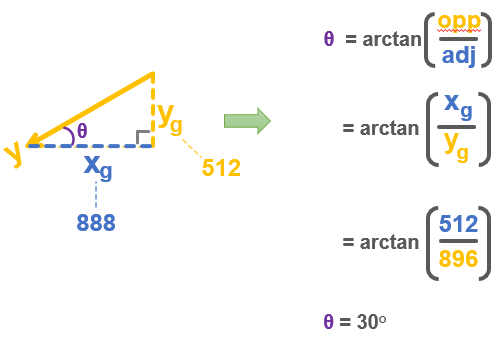
For any angle you rotate to, the micro:bit accelerometer’s x sensing axis will align with gravity by a certain amount (xg), and the y sensing axis will also align by some amount (yg). Let’s say you are holding the micro:bit vertically and have it rotated by 30°. In that case, yg measures about 512, or 0.5 g. (1 g is 1024). xg will be around 888, which is about 0.87 g.
If you look closely, the x and y sensing axis triangles are identical. So, you could take the xg leg from the x-axis triangle and fit it on the adjacent side of the y-axis triangle.
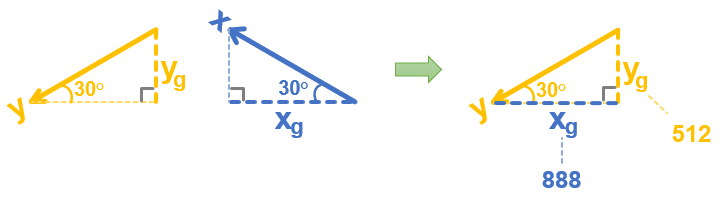
Like the script, if all you know is the x and y axis measurements (xg and yg), you could now use a calculator to figure out the angle θ by taking the arctan of 512 / 888. The result is 29.96, or rounding up, it’s 30.
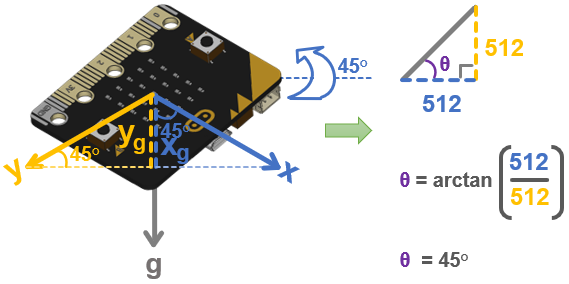
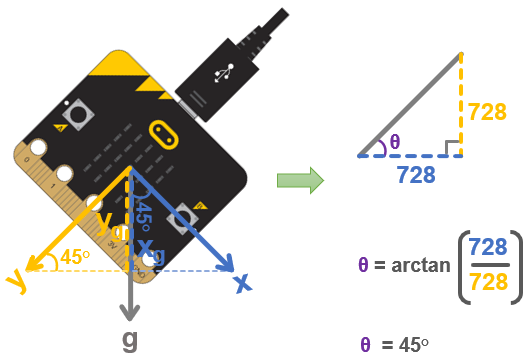
Here is an example where the rotation is 45°. Both x and y report 728, and the arctan(728/728) = arctan(1) = 45.
If you were wondering how the script could calculate the angle even when the micro:bit was tilted, it’s because the portions of the effects on each axis were reduced by the same fraction. When holding vertical, the arctan(728/728) resulted in arctan(1) = 45. Likewise, with the tilt away from you, arctan(512/512) = arctan(1) = 45. In other words, the ratio of the x and y measurements are the same, so the result of the arctan calculation is also the same.