Once your script knows the index of a character in a string, it can simply add the key to the index and use the result to get the ciphertext character.
The first four statements are the same as the previous activity. So when key = 5 and the plaintext letter = M, alpha.find(letter) returns 12, which gets stored in index. Now for the Caesar shift. index = index + key evaluates to index = 12 + 5, which is 17. With result = alpha[index], that’s result = alpha[17]. Since alpha[17] returns "R", that’s the ciphertext character the result variable stores.

Circular Shift and the Modulus (Division Remainder) Calculation
Remember the circular shift? That’s when the next character after Z in a Caesar shift wraps around to A. For example, with a plaintext letter of X and a key of 5, we want a ciphertext letter of C.
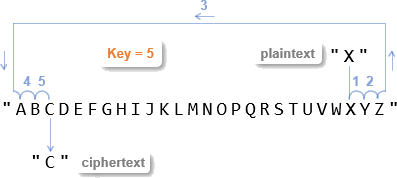
This circular shift is made possible by index = index % 26. The % operator is called the modulus operator, and it returns what’s left over from an integer division operation. Unlike floating point division where 19 / 5 = 3.8, integer division’s quotient result would be 3 with a remainder of 4. Integer division always rounds down, so 19 // 5 = 3. The remainder is 19 % 5 = 4. That remainder of 4 is another way of expressing the 0.8 part of 3.8 because 0.8 * 5 = 4. Another way to think about the remainder is that 3 * 5 = 15, which is 4 below the original numerator of 19.
After index = index + key, 24 is still Y, and 25 is still Z, but 26 isn’t in the alphabet. In fact, alpha[26] would cause an exception in the script by making it look for a character that’s not there. 26 needs to be changed to 0, 27 needs to be changed to 1, 28 needs to be changed to 2 and so on… That’s exactly what index = index % 26 does, as you can see from the right column in this table. It also works fine for values below 26.
Integer quotient, integer remainder
24 // 26 = 0 24 % 26 = 24
25 // 26 = 0 25 % 26 = 25
26 // 26 = 1 26 % 26 = 0
27 // 26 = 1 27 % 26 = 1
28 // 26 = 1 28 % 26 = 2
29 // 26 = 1 29 % 26 = 3
Here is an example with a key of 5 and the plaintext letter X. See how the result of 28 % 26 is 2? The letter C in the alpha string has an index of 2, and that’s the correct result if the script starts with X and a key of 5.

Decrypt with the Same Cipher
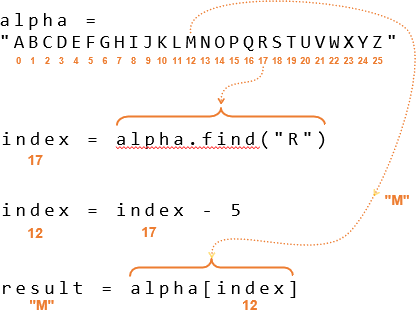
Let’s say your script receives the ciphertext letter R and an encryption key of 5. How would it decrypt to get back to the plaintext letter M?
The answer is to use the same algorithm, but reverse the sign of the key so that it’s -5. The index of R is 17, so index = index + key would be index = 17 + -5 = 12. That’s the index of M, and that’s how the script can use the negative value of a key to decrypt from a ciphertext character back to the original plaintext character.
Your Turn – ROT-13
The ROT-13 cipher is a special case of the Caesar cipher where the characters are shifted right 13 places. Are you ready to create a ROT-13 cipher? Hint: key = 13!
- Set up a ROT-13 cipher, and test with each letter in H E L L O. If you did it correctly, the ciphertext result should be U R Y Y B.
