The rc-time circuits in this tutorial can work under a variety of lighting conditions. Now we need some code that can adapt as well.  An example of script code that cannot adapt to change would be:

if qt_left > 2500)...          # Not good for navigation.

That statement might work well for turning away from shadows in one room, but take it to another with brighter lights, and it might never detect a shadow.  Or, take it to a darker room, and it might think it’s seeing shadows all the time. 

For the cyber:bot to navigate with phototransistors, the exact light levels measured aren't really important. What matters is which sensor detects the brightest light.

The next example script takes a light level measurement from each sensor. Then, it uses an equation to turn the two measurements into a single value between -0.5 and +0.5.   A value of zero means the two photoresistors are detecting equal brightness.

Let's run the script first, then examine what it is doing.

ERROR FALSE ALARM! On line 11 of the script flash norm_diff_shade_value, you may see a compiler error warning "Operator "+" not supported for this combination of types."  This is just a false alarm.  The script actually works just fine, so go ahead and send it to the micro:bit.

Example script: flash norm_diff_shade_value

• Make sure there is no direct sunlight streaming in nearby windows.  Indoor lighting is good, but direct sunlight will still flood the sensors.
• Use the micro:bit Python Editor to open a previous cyber:bot project, like left_light_sensor or cyberbot-template-with-blink.
• Set the project's name to norm_diff_shade_value, update the script so that it matches the one below, and then click Save.
• Click Send to micro:bit.  

# norm_diff_shade_value

from cyberbot import *
 
while True:                       
    bot(8).write_digital(1)        
    qt_left = bot(8).rc_time(1)   
    bot(6).write_digital(1)        
    qt_right = bot(6).rc_time(1)   
    
    norm_diff_shade = (qt_right / (qt_right + qt_left)) - 0.5
    
    display.scroll(norm_diff_shade)            
    sleep(500)

• Set the cyber:bot board's PWR switch to 1.
• Cast shade over the cyber:bot’s right phototransistor.  The the micro:bit should display a positive value; the darker the shade, the larger the value.
• Cast shade over the cyber:bot’s left phototransistor.  The the micro:bit should display a negative value.
• Position the cyber:bot so both phototransistors see about the same level of bright light. The micro:bit should display a value close to 0.
• Cast equal shade over both sensors.  Even though the overall light level dropped, the display should still report a value close to zero.
• Set the cyber:bot board's PWR switch to 0.

How norm_diff_shade_value Works

For navigation, what matters is the difference in how much light the two photoresistors detect, so the robot can turn toward the sensor seeing brighter light (or away from it, depending on what you want.)  The script norm_diff_shade_value finds this difference by dividing the right sensor measurement into the sum of both.  The result will always be in the 0 to 1 range.  This technique is an example of a normalized differential measurement.  Here’s what this technique looks like as an equation:

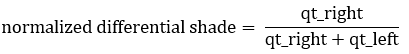
For example, a normalized differential measurement of 0.25 would mean  “the light is 1/2 as bright over the right sensor as it is over the left.” The actual values for qt_right and qt_left might be small in a bright room or large in a dark room, but the answer will still be 0.25 if the light is 1/2 as bright over the right sensor.  A measurement of 0.5 would mean that the qt_right and qt_left values are equal.  They could both be large, or both be small, but if the result is 0.5, it means the sensors are detecting the same level of brightness.

But, the script norm_diff_shade_value adds one more step: it subtracts 0.5 from the normalized differential shade measurement.  That way, the results range from –0.5 to +0.5 instead of 0 to 1, and a measurement of 0 means equal brightness.  The result is a zero-justified normalized differential shade measurement, that looks like this as an equation:
 

But why bother with the extra step? The value range –0.5 to +0.5 is great for navigation scripts because the positive and negative values can be used to scale the wheels speeds.  Here is how the zero-justified normalized differential shade equation appears in the script:

 norm_diff_shade = (qt_right / (qt_right + qt_left)) - 0.5

This line is used in the next two example scripts, which will show its usefulness.