The first portion of the code the same as the script test_accel_xy_angle from the previous activity, only the comment at the beginning has a different name!

# rotate_angle_with_degree_of_tilt

from microbit import *
import math

sleep(1000)

while True:
    x = accelerometer.get_x()
    y = accelerometer.get_y()
    
    angle = round( math.degrees( math.atan2(y, x) ) )

Here is the one line that was added that calculates a number that can be used to indicate the degree of tilt.  It calculates x2 + y2, and then takes the square root of that.  What it’s calculating is the length of the hypotenuse of the triangles introduced in the previous Did You Know? page on trigonometry.  More details are in the next Did You Know? section below.

    hyp = round( math.sqrt( x**2 + y**2 ) )

A print statement was added to show the hypotenuse (hyp) result on another line.

    print("x =", x, ", y =", y, ", angle =", angle)
    print("hyp =", hyp)
    print()

    sleep(750)

Did You Know?

As you’ve seen with the rotate_angle_with_degree_of_tilt script, the micro:bit can report tilt level along with rotation. But is there really a relationship between the rotation angle and the level of tilt?  

The answer is yes.  Just as the x-axis measurement is the adjacent leg of the triangle and the y-axis is the opposite leg, the tilt away from vertical is indicated by the hypotenuse.  

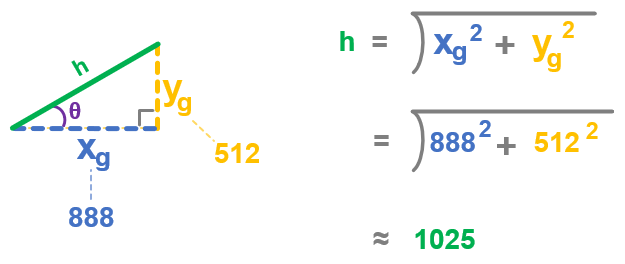
Here’s an example where the hypotenuse is calculated with the 30° values of xg = 888 and yg = 512.  The result is 1025, which is essentially a total of 1g, meaning that the micro:bit is being held vertical.

Here is another example where the hypotenuse is calculated with the rotation of 45°, and tilted away at 45°.  For this, the values of xg = 512 and yg = 512.  The result is 724.  The closer the tilt gets to level, the smaller the hypotenuse value will be.

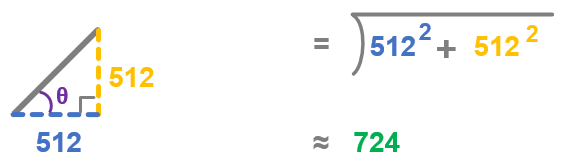
You might encounter this calculation described as a vector magnitude in later physics and engineering classes.